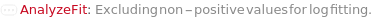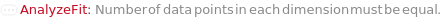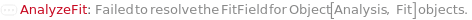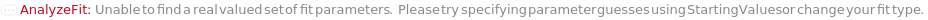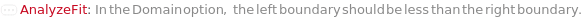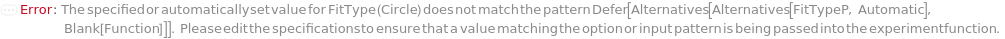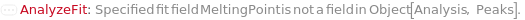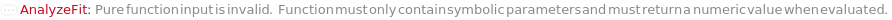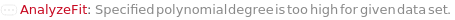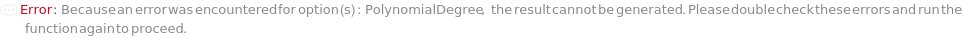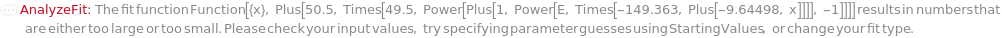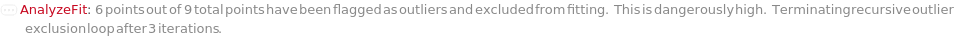AnalyzeFit
AnalyzeFit[Coordinates, FitType]⟹F
fits a function F of type FitType to the given coordinates.
Details
-
CannotFit Unable to find a satisfactory solution. Please try specifying parameter guesses using StartingValues or change your fit type. DataSizeMismatch Number of data points in each dimension must be equal. FitFieldResolutionFailure Failed to resolve the FitField for `1` objects. ImaginaryFitParameters Unable to find a real valued set of fit parameters. Please try specifying parameter guesses using StartingValues or change your fit type. InputDataSizeMismatch Number of input dimensions in data must match number of inputs in pure function. InvalidDomain In the Domain option, the left boundary should be less than the right boundary. InvalidExpressionType Expression type `1` cannot be fit to data with `2` independent variables. InvalidFitField Specified fit field `1` is not a field in `2`. InvalidFunction Pure function input is invalid. Function must only contain symbolic parameters and must return a numeric value when evaluated. InvalidPolynomialDegree Specified polynomial degree is too high for given data set. MachinePrecisionIssue The fit function `1` results in numbers that are either too large or too small. Please check your input values, try specifying parameter guesses using StartingValues, or change your fit type. NonPositiveValues Excluding non-positive values for log fitting. NoUnknownParameter There is no unknown parameter to fit in the given expression. NoValidData No remaining data points after filtering based on Domain, Range, and Exclude options. OverFit You are fitting a function with `1` parameters to `2` data points. Generally speaking, this is not a good idea. It means there are infinite number of fits that will interpolate your data points exactly. One such solution will be returned. Error prediction will not be available in this case. TooManyOutliers `1` points out of `2` total points have been flagged as outliers and excluded from fitting. This is dangerously high. Terminating recursive outlier exclusion loop after `3` iterations. UnusedFitNormalization FitNormalization will rescale the equation parameters only for Exponential, Logistic, LogisticBase10, and GeneralizedLogistic. ZeroInterceptIgnored The ZeroIntercept option can only be used with fit type Linear, but fit type `1` was provided. ZeroIntercept will be ignored.
Input

Output

General Options

Method Options

Messages
Examples
open allclose allAdditional Examples (30)
Fit Type (9)
Multivariate Data (5)
Object inputs (10)
Fit a LogLinear standard curve relating copy number to quantification cycle:
Fit a standard curve relating peak position to fragment size by pulling all x-values from first object and all y-values from second object:
Fit a standard curve to fluorescence intensities data:
Fit a standard curve to fluorescence kinetics data:
Fit function of two variables to fluorescence objects:
Fit function of two variables to peak positions:
Fit Volume vs LiquidLevel using ObjectFields to address multiple fields in the same objects:
Uncertain data (5)
Options (30)
Domain (2)
ErrorMethod (2)
Exclude (2)
ExcludeOutliers (2)
Excluding outliers from a fit often results in new outliers due to the resulting fit being more accurate. ExcludeOutliers->Repeatedly re-fits excluding the newly found outliers up to 3 times or until no more outliers are found:
If ExcludeOutliers->True, any points detected as outliers will be excluded from fitting: